
“ 关于ML树模型在时序方面运用的Post ”#
一、对于单个时序变量的预测,如何进行特征变量的构建#
1. 对时序变量 Y 进行滞后
对于时序变量 Y 进行 滞后N步 ,从而形成一个滞后N期的特征变量,其中该列特征变量的 当前值 与在时序变量 Y 在 时间 t-N的值 一致。
即如果我们对 Y 做一个滞后1步的转移,并在该特征上训练一个模型,则该模型将能够在观察到该系列的当前状态后 提前1步 进行预测。
如果增加滞后期,比如:将滞后步数增加到 7,将允许模型提前7步进行预测。如果在7天前的未观察到的时间里,有某些外部因素从根本上改变了该系列,该模型将无法捕捉到这些变化,并将返回具有较大误差的预测结果。因此,在最初的滞后期选择中,必须在 最佳预测质量和预测范围的长度之间找到一个平衡。
2. 计算观察窗口的统计量
通过设置 N 天的观察窗口 ,通过计算 N 天内 时序变量 Y 的统计量 ,即移动统计量,以此作为当天的特征变量,从而构建出一个特征变量。
例如:假如时序变量是以 “天” 为时间间隔,则我们可以以当前日期往前 7 天作为观察窗口,计算滞后7天至滞后1天内时序变量 Y 的方差,以此作为当前值所对应的一个特征值。使用该特征训练模型,则该模型将能够观察到该时序变量 Y 的当前状态的 前 7 天的波动情况 ,以此进行预测。
除了方差之外,我们也可以选择观测窗口中的最大值、最小值、平均值、中位数等统计量作为特征值,并且每个特征值所解释的效果会有所不同,甚至也可以改变窗口内每一期的权重从而计算。
3. 给日期和时间进行标记
对于时间为具体日期或者时间的时序变量,我们可以对具体时间贴上标签,并转化为布尔值或者数值从而构建出特征值。
例如:时间是具体的日期,时序变量 Y 为商城的人流量,则我们可以对 Y 所对应的每个具体日期按周标记或者特殊节假日标记,比如对每个日期是一周中的第几天并对其进行标记;或者该日期是否对应特殊的节假日,并将其标记为布尔值,从而构建出新的特征值。使用该特征训练得到的模型,将能够观察到工作日和周末、节假日对时序变量 Y 带来的影响。
除此之外,面对不同类型的数据,我们还可以标记年份、季节、月份、一小时中的分钟、一天中的小时、特殊事件的发生等等以此类推,不同的标记会使模型观察得到不同的效果,可以根据预测效果的质量,设置标签,从而帮助模型优化预测效果。
二、 树模型XGBoost在时间序列的运用例子#
下例子使用的时序变量 Y 为PJM东部地区2001-2018年的每小时能耗。
1. 导入包
1
2
3
4
5
6
7
| import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import xgboost as xgb
from xgboost import plot_importance, plot_tree
from sklearn.metrics import mean_squared_error, mean_absolute_error
|
2. 读取数据、区分验证集和训练集
1
2
3
4
5
6
7
8
9
10
| pjme = pd.read_csv('../input/PJME_hourly.csv', index_col=[0], parse_dates=[0])
# 以2015年作为训练集和验证集的分割点
split_date = '01-Jan-2015'
pjme_train = pjme.loc[pjme.index <= split_date].copy()
pjme_test = pjme.loc[pjme.index > split_date].copy()
# 绘制数据的观测图
color_pal = ["#F8766D", "#D39200", "#93AA00", "#00BA38", "#00C19F", "#00B9E3", "#619CFF", "#DB72FB"]
_ = pjme.plot(style='.', figsize=(15,5), color=color_pal[0], title='PJM East')
|
结果如下(可以看出基本为平稳序列):

3. 读取数据,构建特征变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| # 以拆分、标记时间日期作为特征值
def create_features(df, label=None):
df['date'] = df.index
df['hour'] = df['date'].dt.hour
df['dayofweek'] = df['date'].dt.dayofweek
df['quarter'] = df['date'].dt.quarter
df['month'] = df['date'].dt.month
df['year'] = df['date'].dt.year
df['dayofyear'] = df['date'].dt.dayofyear
df['dayofmonth'] = df['date'].dt.day
df['weekofyear'] = df['date'].dt.weekofyear
X = df[['hour','dayofweek','quarter','month','year',
'dayofyear','dayofmonth','weekofyear']]
if label:
y = df[label]
return X, y
return X
X_train, y_train = create_features(pjme_train, label='PJME_MW')
X_test, y_test = create_features(pjme_test, label='PJME_MW')
|
4. 建立和训练模型
1
2
3
4
5
| reg = xgb.XGBRegressor(n_estimators=1000)
reg.fit(X_train, y_train,
eval_set=[(X_train, y_train), (X_test, y_test)],
early_stopping_rounds=50,
verbose=False)
|
5. 在验证集上验证结果
1
2
3
4
| pjme_test['MW_Prediction'] = reg.predict(X_test)
pjme_all = pd.concat([pjme_test, pjme_train], sort=False)
# 结果可视化
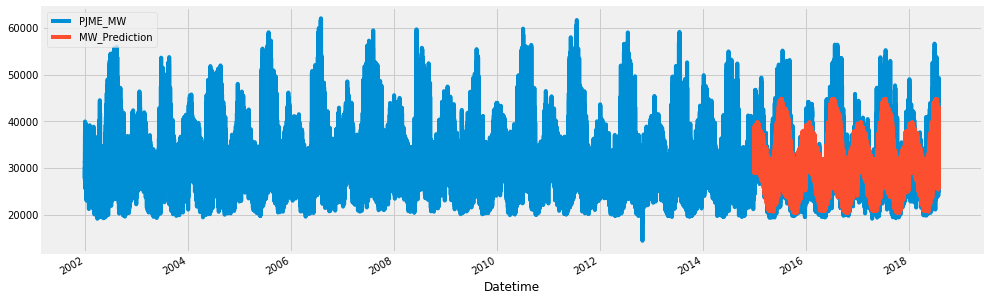
pjme_all[['PJME_MW','MW_Prediction']].plot(figsize=(15, 5))
|
结果如下:
6. 输出模型在验证集上的均方误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)
- 均方误差计算公式:$MSE=\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y_{i}})^2$
- 平均绝对误差计算公式:$MAE =\frac{\sum_{i=1}^{n}|y_i-\hat{y_i}|}{n}$
- 平均百分比误差计算公式:$\frac{100}{n}\sum_{i=1}^n\frac{|y_i-\hat{y_i}|}{y_i}$
1
2
3
4
5
6
7
8
9
10
11
12
13
| # 均方误差
mean_squared_error(y_true=pjme_test['PJME_MW'],
y_pred=pjme_test['MW_Prediction'])
# 平均绝对误差
mean_absolute_error(y_true=pjme_test['PJME_MW'],
y_pred=pjme_test['MW_Prediction'])
# 平均绝对百分比误差
def mean_absolute_percentage_error(y_true, y_pred):
"""Calculates MAPE given y_true and y_pred"""
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
mean_absolute_percentage_error(y_true=pjme_test['PJME_MW'],
y_pred=pjme_test['MW_Prediction'])
|
结果为:RMSE 为 13780445;MAE 为2848.89;MAPE 为*8.9%


