ML：自编码器（AutoEncoder）在降维中的作用

(1) 简介

在深度学习中，自动编码器是一种无监督的神经网络模型，由编码器组件和解码器组件组成，编码器(encoder)获取输入向量并将其转换为压缩编码（code），然后交给解码器(decoder)。解码器力求尽可能训练模型以接近并重建原始的输入向量。

自动编码器可以用于特征降维，类似主成分分析PCA，但是其相比PCA其性能更强，在机器学习中不仅可以减少问题的维数，同时可以将数据集中的噪声去除。

除了进行特征降维，自动编码器学习到的新特征可以送入有监督学习模型中，所以自动编码器可以起到特征提取器的作用。

(2) 运作的过程

现在让巨弱举个简单的例子，具体说说自编码器是如何在降维中发挥作用的，以及的运作原理过程。以下图为例：

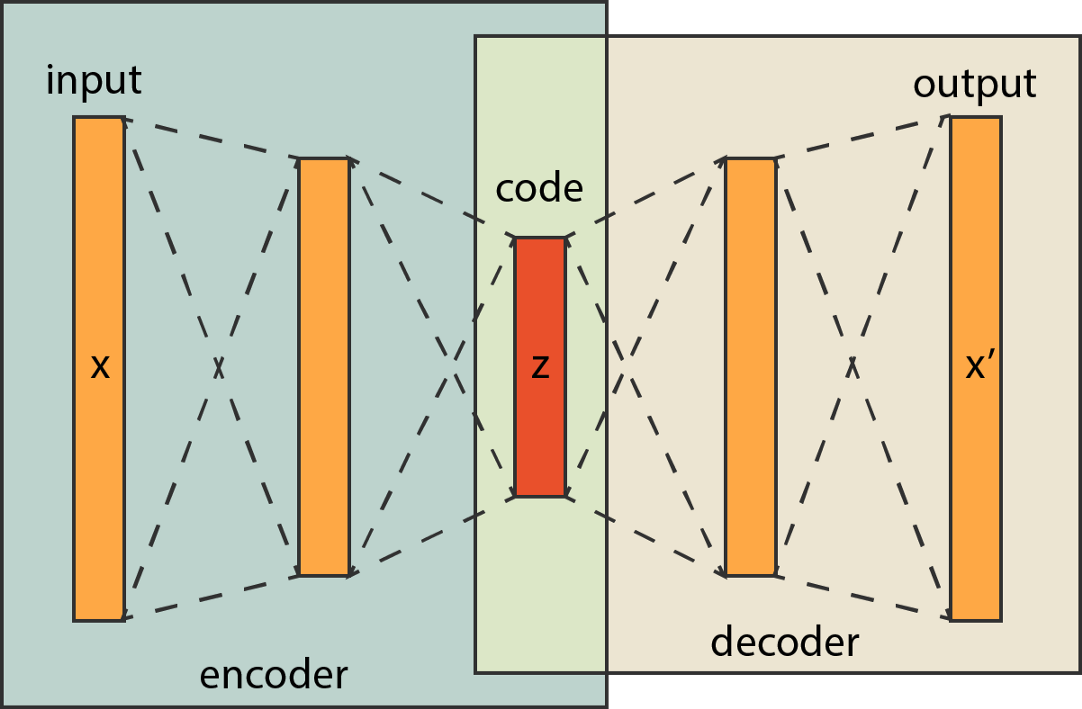
1. 先来看编码encoder部分：

encoder 是一个降维的过程。

Input 是每个样本的特征向量 $[x_1,x_2,x_3\dots x_k]$ 也叫做 k 维特征向量，其中 $x_i$ 是该样本的第 i 个变量的值，code 部分为以 input 作为输入向量经过层层神经元后得到的 z 维输出向量，即也可以称为降维后的 z 维向量，z < k；

2. 再看解码decoder部分：

decoder是用来升至原来维度，并尽可能使升维结果与原始数据一致，以此训练出含有信息最多的最优降维输入。

在解码部分中，模型以code（encoder输出的低维向量结果）作为decoder部分输入的特征向量，再经过 decoder 的层层神经元拟合计算，得到最终的 output向量，output的维度也为 k。

3. 最后我们解 encoder 与 decoder结合起来看：

在整个编码解码的过程中，神经网络以每个样本的 k 维特征向量作为输入，同样以每个样本的 k 维特征向量作为模型需要拟合的输出结果，而中间作为衔接 encoder 与 decoder 的 code 部分则是降维的结果。

模型先将样本的 k 维特征向量进行训练输出为 z 维的 code 向量;
以 z 维的 code 特征向量作为后半部分模型的信息输入，训练输出 output 向量与 input 的样本特征向量进行比对;
通过损失函数最小化，不断训练两部分的神经元参数，以此得到与input 相差最小的 output 向量，此时 code 的 z 维向量即为承载着 input（样本的k维向量） 信息量最多的低维向量。
通过自编码器训练得到的模型，我们只需取encoder部分，将样本的特征向量进行输入，即可得到承载信息量最多的 z 维向量。即达到了降维的效果。

注意：虽然自编码器在大部分时候的降维效果都非常不错，但是该方法无法对降维后的向量赋予实际意义进行解释，只知道降维后的向量继承了原向量最多的信息量，说明该降维得到的向量对原向量具有很强的解释性。因此对于需要提供解释的问题，该类方法不太适用。

(3) 自编码器代码如下

巨弱使用了此学期《多元统计分析》中的 case4 数据集进行试验。

1. 导入必要库

1
2
3
4
5
6
7
8
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.layers import Dense
import random
from sklearn.preprocessing import StandardScaler

2. 定义一个绘制自编码器的拟合效果图函数：

随机选择三个样本进行特征向量的原始值和模型的构建值的拟合图绘制

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
# 定义一个绘制自编码器的拟合效果图函数
# n_sample = 3 表示抽取3个样本进行拟合效果比较，也可以进行修改
def plot_orig_vs_recon(x_train, col_names,, xtick, autoencoder, title='', n_samples=3):
    fig = plt.figure(figsize=(10,6))
    plt.suptitle(title)
    for i in range(3):
        plt.subplot(3, 1, i+1)
        idx = random.sample(range(x_train.shape[0]), 1)
        plt.plot(autoencoder.predict(x_train[idx]).squeeze(),
                                     label='reconstructed' if i == 0 else '')
        plt.plot(x_train[idx].squeeze(), label='original' if i == 0 else '')
        fig.axes[i].set_xticklabels(col_names)
        plt.xticks(np.arange(0, xtick, 1))
        plt.grid(True)
        if i == 0: 
            plt.legend()

3. 定义自编码器的结构：

以下函数的参数意义为：

df：原始数据集；
col_names：需要进行降维的特征名称；
input_dim：输入的特征维度；
coder_dim：降维得到的维度；

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 定义一个绘制自编码器的拟合效果图函数
def auto_encode(df, col_names, input_dim, code_dim):
    df = df[col_names]
    x_train = df.to_numpy()

    # 数据标准化
    scaler = StandardScaler()
    scaler.fit(x_train)
    x_train = scaler.transform(x_train)

    # 定义编码器与解码器（结构可以根据效果进行修改）
    encoder = Sequential([
        Dense(6, activation='relu', input_shape=(input_dim,)),
        Dense(code_dim, activation='relu')
    ])

    decoder = Sequential([
        Dense(6, activation='relu', input_shape=(code_dim,)),
        Dense(input_dim, activation=None)
    ])

    # 合并成自动编码器（损失函数选择均方）
    autoencoder = Model(inputs=encoder.input, outputs=decoder(encoder.output))
    autoencoder.compile(loss='mse', optimizer='adam')
    # 自编码器进行训练（epoch，我这里默认了1500次，根据收敛进行修改）
    model_history = autoencoder.fit(x_train, x_train, epochs=1500, batch_size=32, verbose=0)

    # 输出损失值，并将其可视化
    plt.plot(model_history.history["loss"])
    plt.title("Loss vs. Epoch")
    plt.ylabel("Loss")
    plt.xlabel("Epoch")
    plt.grid(True)

    # 绘制拟合效果图
    plot_orig_vs_recon(x_train, col_names, input_dim, autoencoder, title = '自编码器降维重构后的效果')
    # 返回得到的编码器（降维模型）
    return encoder, x_train

4. 使用模型输出降维结果

以下是巨弱使用了一个巨弱本人正在上的课程《多元统计分析》中的case4案例数据集进行了测试，数据中需要降维的特征变量名为 $[x1,x2,x3,\dots,x9]$ ，即输入维度为9，巨弱试验的降维维度为 2

1
2
3
# 读取数据
case2 = pd.read_excel('mvstats5.xlsx', sheet_name = 'd10.2')
case2.shape

结果为：(31,7)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
col_names, input_dim, code_dim = case4.columns[1:], 6, 2

# 训练模型
encoder, x_train =  auto_encode(case4, col_names, input_dim, code_dim)

# 输出降维结果
encoded_x_train = encoder(x_train)
# 可视化降至2维的特征结果
plt.figure(figsize=(6,6))
plt.scatter(encoded_x_train[:, 0], encoded_x_train[:, 1], alpha=.8)
plt.xlabel('Latent Dimension 1')
plt.ylabel('Latent Dimension 2')

下图为训练过程终损失值的变化，可以看出损失值最终收敛于很小的数值

损失值.png

下图为自动编码器重构数据集后与原数据的拟合对比图，可以看出重构的效果非常不错，说明降维后的数据保存了原数据的大部分信息量。

autoencoder拟合.png

下图为自动编码器对数据集进行降维后，得到的 2 维散点图。

autoencoder降维.png

(4) 其他类型的自编码器

机器学习中除了以上传统的自编码器外，还有两种更为高级的自编码器，但是巨弱认为在一般的统计实验中使用传统的自编码器完全够用

1. 卷积自编码器

卷积自编码器使用卷积层和池化层替代了原来的全连接层，能够对高维图像进行处理降维，并且尽可能少的减少信息损失。

传统自编码器一般使用的是全连接层，对于一维信号并没有信息损的影响，而对二维图像，全连接层会损失空间信息，因此相对于传统自编码器，卷积自编码器能够通过卷积操作，很好的保留二维信号的空间信息。

2. 正则自编码器（去噪编码器）

去噪自编码器是一类接受损坏数据作为输入，并训练来预测原始未受损数据作为输出的自编码器（相当于增加了正则项）。

在将输入传递到网络之前添加噪声，因此如果它是图像，也许你添加了模糊，然后你让网络学习如何消除你刚刚增加的噪声并重建原始输入，这样重建误差就会稍微变小。去噪自动编码器可以通过卷积层来增强，以产生更有效的结果。

(5) PCA与自编码器的简单对比

自动编码器和 PCA 都可以用作降维技术。但是两者之间存在一些差异：

根据定义，PCA 是一种线性变换，而 auto-encoder 能够对复杂的非线性函数进行建模。然而，内核 PCA可以对非线性数据进行建模。
在 PCA 中，根据定义，特征是线性不相关的，它们是正交基础上的投影。相反，自动编码的特征可能是相关的。这两个优化目标完全不同（当数据投影到其上时最大化方差的正交基与最大精度重建）。

(1) 简介#

(2) 运作的过程#

(3) 自编码器代码如下#

(4) 其他类型的自编码器#

(5) PCA与自编码器的简单对比#

(1) 简介

(2) 运作的过程

(3) 自编码器代码如下

(4) 其他类型的自编码器

(5) PCA与自编码器的简单对比